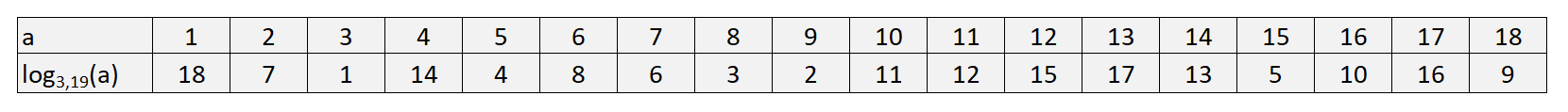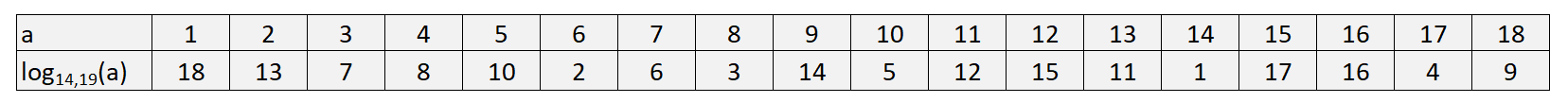$$\log_x​(x) = 1$$

The discrete logarithmic problem is a hard problem that has been used in the design and implementation of encryption algorithms in cryptography. Before we outline the hard problem, let's first recap some of the foundational mathematical concepts.

According to Euler's totient function, the following holds true:

$$a^{ϕ(n)} ≡ 1 \mod n$$

Where a and n are relatively prime integers and Φ(n) represents the number of positive numbers less than n that are relatively prime to n.

We can rewrite the equation as follows:

$$a^m ≡ 1\mod n$$

Where m = Φ(n), and can be defined as:

• the order of a (mod n)

• the exponent to which a belongs to (mod n)

• the length of the period generated by a.

The description of m here is of particular importance. To illustrate this better, consider the image shown below, which outlines all the powers of a mod 19.

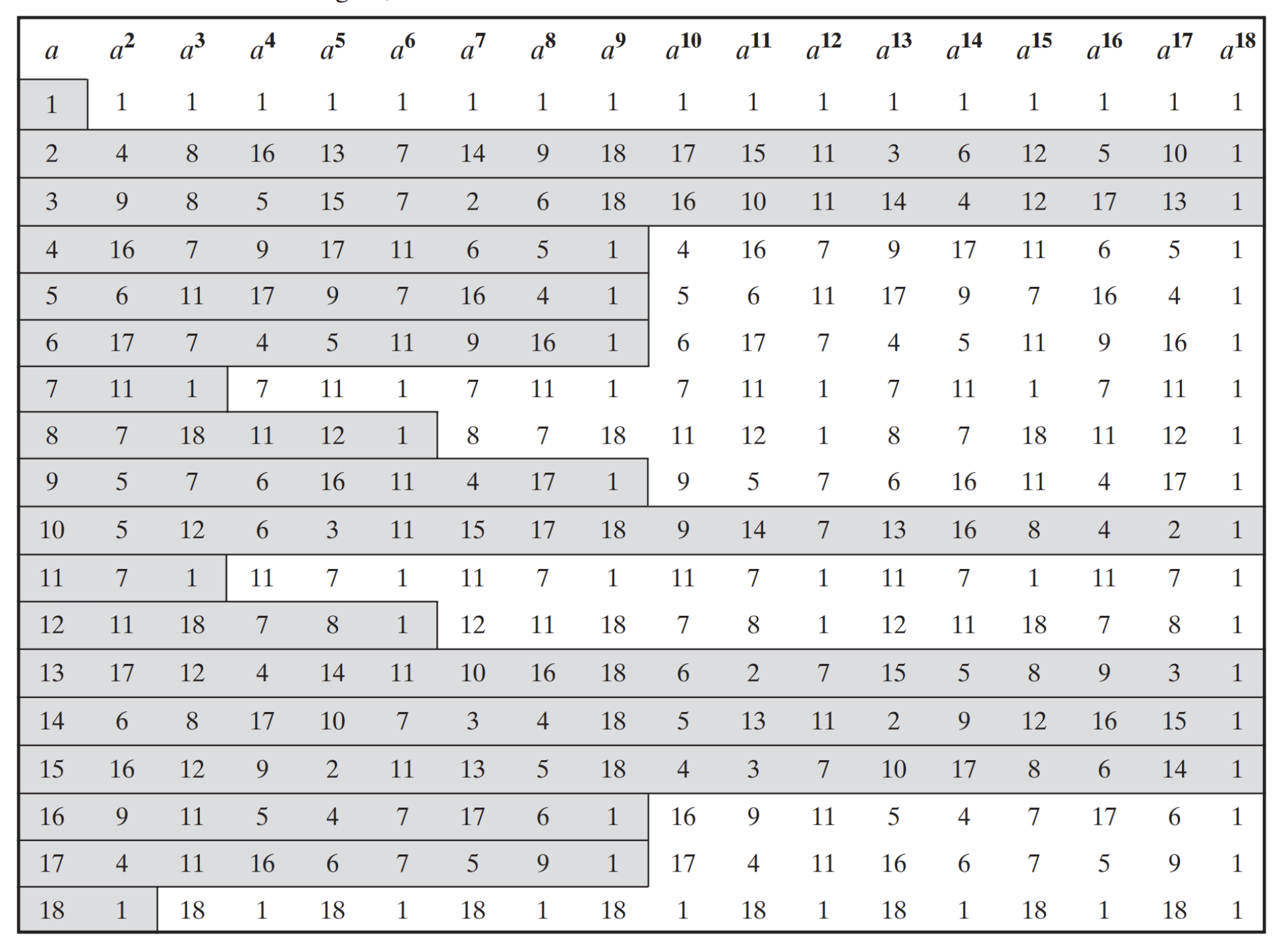
What we can observe in the image is that for a given simplistic n = 19, since n is prime, all numbers less than n are relatively prime to n. Furthermore, for every value assigned to a < 19, we can obtain the residue modulo n. What is important to note is that after a certain number of executions, the residue pattern repeats. If it is not obvious, take a closer look at the shaded component in the image for each line. The shaded component represents the repeating residue pattern.

Extending this further, we can stipulate that Φ(n) is the maximum possible exponent that can belong to a number. However, as evident in the image above, the maximum exponent doesn't necessarily guarantee a residue pattern that doesn't repeat. When a number does have a residue pattern of the order Φ(n), this number is called the primitive root of n. This implies that if a is a primitive root of n, then

$$a, a^2, a^3, ... , a^{ϕ(n)}$$

are all distinct (mod n) and are also relatively prime to n.

From this we can note that primitive roots for 19 are 2, 3, 10, 13, 14, and 15.

Note: It is important to note that not all integers will have primitive roots.

Logarithmics for modular arithmetic

Generally, the calculation of the log is the inverse of the exponentiation function.

$$y = x\log⁡_x(y)$$

The above equation defines the calculation of a log for a value y, and a base x, where x > 1.

Furthermore, the following properties pertaining to logarithms hold:

$$\log⁡_x(1) = 0$$

$$\log⁡_x(x) = 1$$

$$\log⁡_x(yz) = \log⁡_x(y) + \log_⁡x(z)$$

$$log⁡_x(yr) = r ⋅ log⁡_x(y)$$

Applying this to the earlier concept of primitive roots, we know that a primitive root a for some prime number p produces a residue ranging from 1 to (p - 1) exactly once for all values of a from 1 to (p - 1). Hence, applying Euler's totient function again, we know that there exists some b, such that

b ≡ r (mod p)   for some r, where 0 ≤r ≤(p − 1)b ≡ r (mod p)   for some r, where 0 ≤r ≤(p − 1)

From modular arithmetic, we can further stipulate that there exists some exponent i for a primitive root a of p, such that

b ≡ ai (mod p)  , where 0 ≤i ≤(p − 1)b ≡ ai (mod p)  , where 0 ≤i ≤(p − 1)

From this calculation, we refer to exponent i as the discrete logarithm of the number b for the base a (mod p). We denote this as

$$d\log⁡_{a,p}(b)$$

Consider the following scenario for some prime p and a primitive root a.

$$x = ad\log⁡_{a,p}(x) \mod p  $$$$   y = ad\log⁡_{a,p}(y) \mod p $$$$    xy = ad\log⁡_{a,p}(xy) \mod p$$

Following modular arithmetic multiplication rules:

$$xy \mod p = [(x \mod p)(y \mod p)] \mod p$$

 $$ad\log⁡_{a,p}(xy) \mod p = [(ad\log⁡_{a,p}(x) \mod p)(ad\log⁡_{a,p}(y) \mod p)] \mod p $$

 adlog⁡a,p(xy) mod p = (adlog⁡a,p(x)+dlog⁡a,p(y)) mod p adloga,p​(xy) mod p = (adloga,p​(x)+dloga,p​(y)) mod p

But revisiting Euler's theorem again:

aϕ(n) ≡ 1 (mod n)

Any z, a positive integer, can be represented as follows:

z = q +kϕ(n)   , 0 ≤q <ϕ(n)

Therefore,

az = aq (mod n)    , if z ≡ q (mod ϕ(n))

Applying the above to the preceding equation:

dlog⁡a,p(xy) ≡ dlog⁡a,p(x) + dlog⁡a,p(y)

Generalising the above we obtain:

dlog⁡a,p(yr) ≡ r ⋅ dlog⁡a,p(y)

Discrete logarithmic problem

Applying the above to determine the discrete logarithm for all the primitive roots of 19, we obtain the following:

• Discrete log to base 2, modulo 19

• Discrete log to base 3, modulo 19

• Discrete log to base 10, modulo 19

• Discrete log to base 13, modulo 19

• Discrete log to base 14, modulo 19

• Discrete log to base 15, modulo 19

From this, we can observe that in order to calculate the discrete logarithm we perform the following calculation for some base g, exponent x, and prime p:

y ≡ gx mod py ≡ gx mod p

We can easily observe that given the values of g, x, and p, it is relatively easy to determine the value of y. However, the discrete logarithmic problem stipulates that, given y, g, and p, it is difficult to determine the value of x.

The magnitude of difficulty is comparable to the integer factorisation algorithms, but the rationale behind using the discrete logarithmic problem to design cryptographic algorithms is that, unlike the integer factorisation algorithm, which can be implemented on a quantum computer, no known algorithm exists to solve the discrete logarithmic problem in P.