Perceptrons traditionally used the (binary) Heaviside step function. The binary threshold was meant to model the way biological neurons ‘fire’. Alternatively, sigmoid can be used.

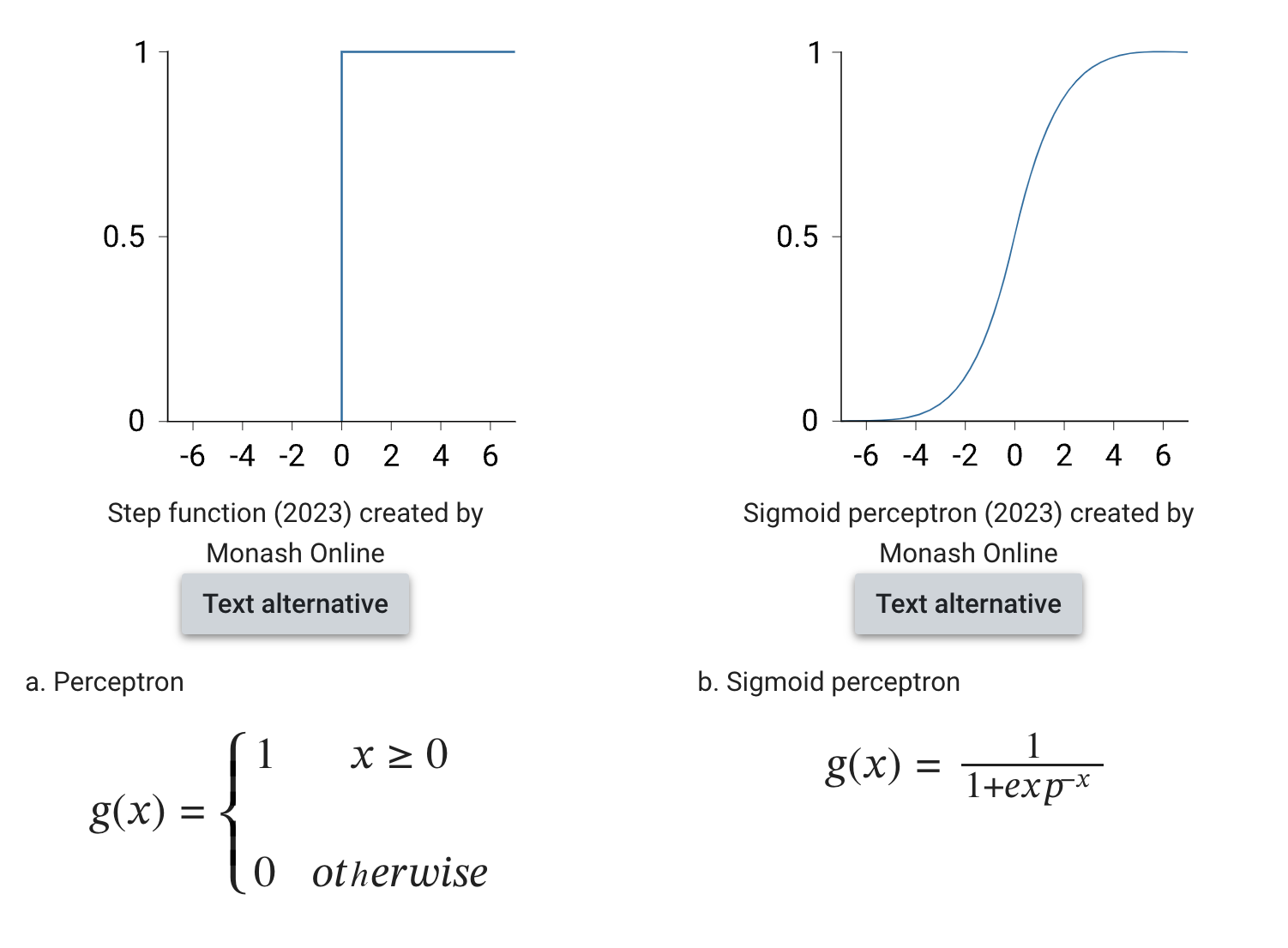
In the context of perceptrons and neural networks, using different activation functions like the step function and the sigmoid function serves different purposes. Here’s a detailed explanation:

Step Function:

• Binary Activation: The step function, also known as the Heaviside step function, outputs either 0 or 1 depending on whether the input is below or above a certain threshold.
• Threshold-based Firing: This mimics the binary “firing” of a biological neuron, where the neuron either fires (1) or doesn’t fire (0).
• Mathematical Simplicity: It’s mathematically simple and computationally efficient.

• Limitations: The step function is not differentiable, which makes it unsuitable for gradient-based optimization methods like backpropagation used in training neural networks.

Sigmoid Function:

• Smooth Activation: The sigmoid function outputs a continuous value between 0 and 1, giving a probabilistic interpretation of the neuron’s activation.
• Differentiability: The sigmoid function is differentiable, which is essential for gradient-based optimization techniques.
• Gradual Response: Instead of a binary output, the sigmoid provides a smooth, gradual response to the input. This allows for more nuanced learning.
• Vanishing Gradients: One downside is that it can suffer from the vanishing gradient problem, where gradients become very small for large input values, slowing down learning.

Why Use the Sigmoid Function?

1. Gradient-Based Learning:

   • Neural networks are typically trained using gradient-based optimization algorithms like backpropagation.
   • The sigmoid function is differentiable, allowing the calculation of gradients needed for these algorithms.

2. Probabilistic Interpretation:

   • The sigmoid function maps any real-valued number into the range (0, 1), which can be interpreted as a probability.
   • This is useful in applications like binary classification, where the output can be interpreted as the probability of belonging to a certain class.

3. Smooth Transitions:

   • Unlike the step function, the sigmoid function allows for smooth transitions between output values, which can be beneficial in learning complex patterns in the data.

Practical Considerations

• Historical Use: The sigmoid was widely used in early neural networks due to its probabilistic output and differentiability.
• Current Trends: Modern neural networks often use other activation functions like ReLU (Rectified Linear Unit), which mitigates some of the sigmoid’s drawbacks, such as the vanishing gradient problem.

Summary

• The step function is simple and mimics binary firing but lacks differentiability.
• The sigmoid function provides a smooth, probabilistic output and is differentiable, making it suitable for gradient-based learning methods despite some limitations like vanishing gradients.
• The choice of activation function depends on the specific requirements of the neural network and the problem being solved.