Rule

$$\int_a^b𝑓’(𝑥)𝑑𝑥=[𝑓(𝑥)+𝑐]_a^b=(𝑓(𝑏)+𝑐)−(𝑓(𝑎)+𝑐)=𝑓(𝑏)−𝑓(𝑎)$$

Explanation

There are many types of integrals, the main types are: definite and indefinite integrals.

Let’s understand these 2 types through an example.

Assume we have a function $𝑓=𝑥^2$, which results with 𝑓′=2𝑥. If $𝑓=𝑥^2+5$, still 𝑓′=2𝑥, and this could be valid for any constant value found in 𝑓.

Therefore, if we are given 𝑓′=2𝑥 to calculate the integral, producing $𝑓=𝑥^2$ might lead to an error since we have no clue about the constant values associated with the function. Hence, we say such integrals are indefinite. In order to overcome this problem, we simply add a constant 𝑐𝑐 at the end of the formula of the function, i.e. $𝑓=𝑥^2+𝐶$,𝐶can be any value including 0.

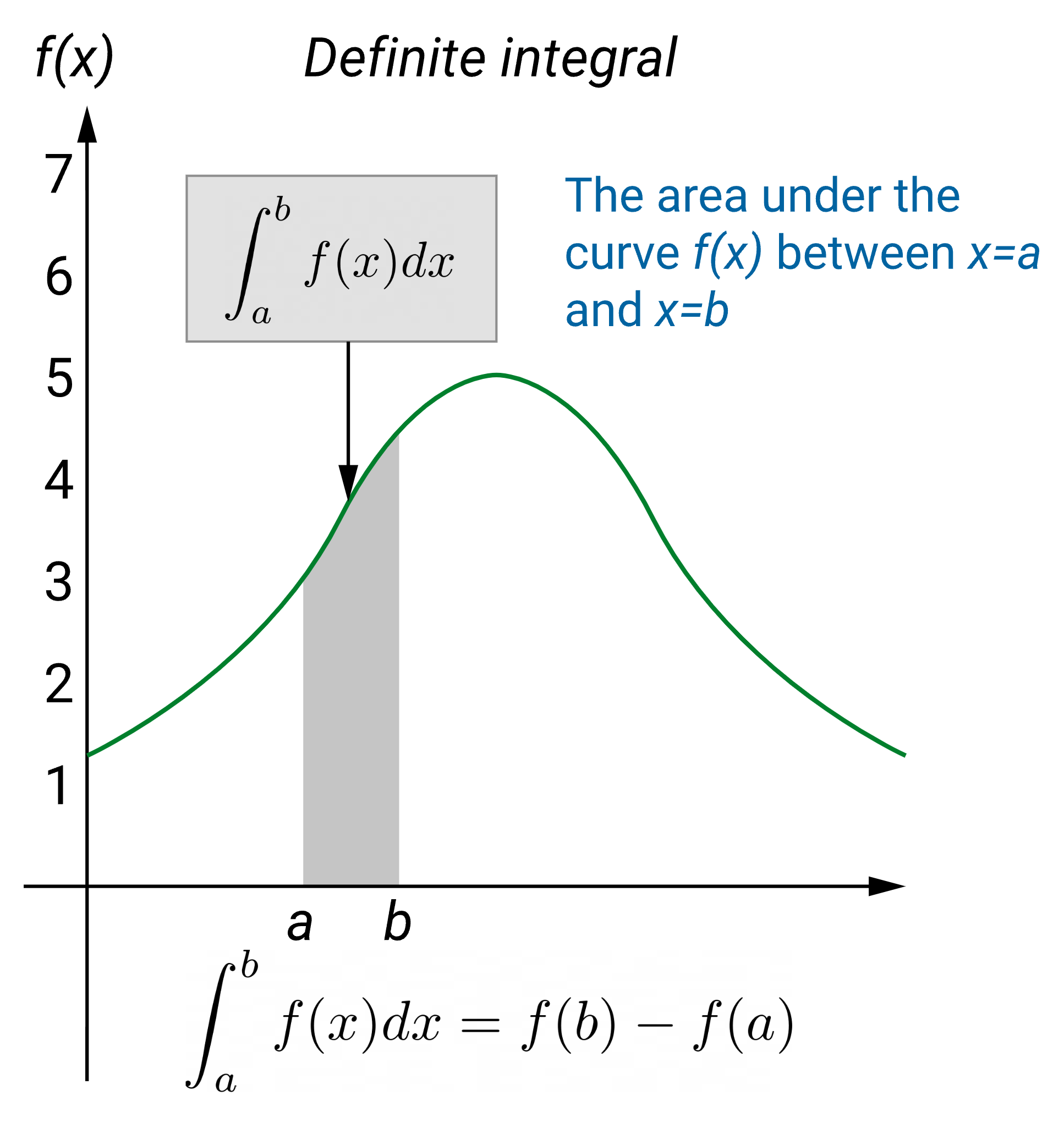
The other type is definite integrals, in which such constraint is not present. In some situations, we might be asked to find the integral between a certain range, for example, $\int_a^b 𝑓’(𝑥)dx$. In such situations, we have to find two integrals first, i.e. when $𝑥=𝑎$ (which is $𝑓(𝑎)$) and $𝑥=𝑏$ (which is $𝑓(𝑏)$), and afterwards find their difference $𝑓(𝑏)−𝑓(𝑎)$ (here $𝑏>𝑎$). When subtracting the two components, the constant value will be cancelled and therefore, we will be able to produce a definite solution. Hence, such types are called definite integrals. Consider the following graph which provides a visual representation of a definite integral.