Meri Leeworthy

Lets read the BeeKEM code 

/// A PathChange represents an update along a path from a leaf to the root.
/// This includes both the new public keys for each node and the keys that have
/// been removed as part of this change.
#[derive(Debug, Clone, Hash, PartialEq, Eq, Deserialize, Serialize)]
#[cfg_attr(any(test, feature = "arbitrary"), derive(arbitrary::Arbitrary))]
pub struct PathChange {
    pub leaf_id: IndividualId,
    pub leaf_idx: u32,
    pub leaf_pk: NodeKey,
    // (u32 inner node index, new inner node)
    pub path: Vec<(u32, InnerNode)>,
    pub removed_keys: Vec<ShareKey>,
}
pub enum NodeKey {
    ShareKey(ShareKey),
    ConflictKeys(ConflictKeys),
}
pub struct ConflictKeys {
    pub first: ShareKey,
    pub second: ShareKey,
    pub more: Vec<ShareKey>,
}
#[derive(Debug, Clone, PartialEq, Eq, Deserialize, Serialize, Hash)]
pub(crate) struct BeeKem {
    doc_id: DocumentId,
    /// The next [`LeafNodeIndex`] available for adding a new member.
    next_leaf_idx: LeafNodeIndex,
    leaves: Vec<Option<LeafNode>>,
    inner_nodes: Vec<Option<InnerNode>>,
    tree_size: TreeSize,
    id_to_leaf_idx: BTreeMap<IndividualId, LeafNodeIndex>,
    /// The leaf node that was the source of the last path encryption, or [`None`]
    /// if there is currently no root key. This is used to determine when a
    /// decrypter has intersected with the encrypter's path.
    current_secret_encrypter_leaf_idx: Option<LeafNodeIndex>,
}
impl BeeKem {
    pub(crate) fn new(
        doc_id: DocumentId,
        initial_member_id: IndividualId,
        initial_member_pk: ShareKey,
    ) -> Result<Self, CgkaError> {
        let mut tree = Self {
            doc_id,
            next_leaf_idx: LeafNodeIndex::new(0),
            leaves: Vec::new(),
            inner_nodes: Vec::new(),
            tree_size: TreeSize::from_leaf_count(1),
            id_to_leaf_idx: BTreeMap::new(),
            current_secret_encrypter_leaf_idx: None,
        };
        tree.grow_tree_to_size();
        tree.push_leaf(initial_member_id, initial_member_pk.into());
        Ok(tree)
    }
fn grow_tree_to_size(&mut self) {
        self.leaves
            .resize(self.tree_size.leaf_count() as usize, None);
        self.inner_nodes
            .resize(self.tree_size.inner_node_count() as usize, None);
    }
    /// Add a new leaf to the first available [`LeafNodeIndex`] on the right and
    /// blank that leaf's path to the root.
    pub(crate) fn push_leaf(&mut self, id: IndividualId, pk: NodeKey) -> u32 {
        self.maybe_grow_tree(self.next_leaf_idx.u32());
        let l_idx = self.next_leaf_idx;
        self.next_leaf_idx += 1;
        self.insert_leaf_at(l_idx, id, pk);
        self.id_to_leaf_idx.insert(id, l_idx);
        self.blank_path(treemath::parent(l_idx.into()));
        l_idx.u32()
    }
    /// Growing the tree will add a new root and a new subtree, all blank.
    fn maybe_grow_tree(&mut self, new_count: u32) {
        if self.tree_size >= TreeSize::from_leaf_count(new_count) {
            return;
        }
        self.tree_size.inc();
        self.grow_tree_to_size();
    }
    fn insert_leaf_at(&mut self, idx: LeafNodeIndex, id: IndividualId, pk: NodeKey) {
        let leaf = LeafNode { id, pk };
        self.leaves[idx.usize()] = Some(leaf);
    }
{
	"versionAtEmbed": "0.3.3",
	"filepath": "assets/Ink/Drawing/2025.6.12 - 13.20pm.drawing",
	"width": 500,
	"aspectRatio": 1
}
    fn blank_path(&mut self, mut idx: InnerNodeIndex) {
        while !self.is_root(idx.into()) {
            self.blank_inner_node(idx);
            idx = treemath::parent(idx.into());
        }
        self.blank_inner_node(idx);
        self.current_secret_encrypter_leaf_idx = None;
    }
    pub(crate) fn contains_id(&self, id: &IndividualId) -> bool {
        self.id_to_leaf_idx.contains_key(id)
    }

    pub(crate) fn node_key_for_id(&self, id: IndividualId) -> Result<NodeKey, CgkaError> {
        let idx = self.leaf_index_for_id(id)?;
        self.node_key_for_index((*idx).into())
    }
    pub(crate) fn leaf_index_for_id(&self, id: IndividualId) -> Result<&LeafNodeIndex, CgkaError> {
        self.id_to_leaf_idx
            .get(&id)
            .ok_or(CgkaError::IdentifierNotFound)
    }
    fn node_key_for_index(&self, idx: TreeNodeIndex) -> Result<NodeKey, CgkaError> {
        Ok(match idx {
            TreeNodeIndex::Leaf(l_idx) => self
                .leaf(l_idx)
                .as_ref()
                .ok_or(CgkaError::ShareKeyNotFound)?
                .pk
                .clone(),
            TreeNodeIndex::Inner(i_idx) => self
                .inner_node(i_idx)
                .as_ref()
                .ok_or(CgkaError::ShareKeyNotFound)?
                .node_key(),
        })
    }
/// TreeNodeIndex references a node in a tree.
#[derive(Debug, Clone, Copy, Hash, PartialEq, Eq, Serialize, Deserialize)]
pub enum TreeNodeIndex {
    Leaf(LeafNodeIndex),
    Inner(InnerNodeIndex),
}

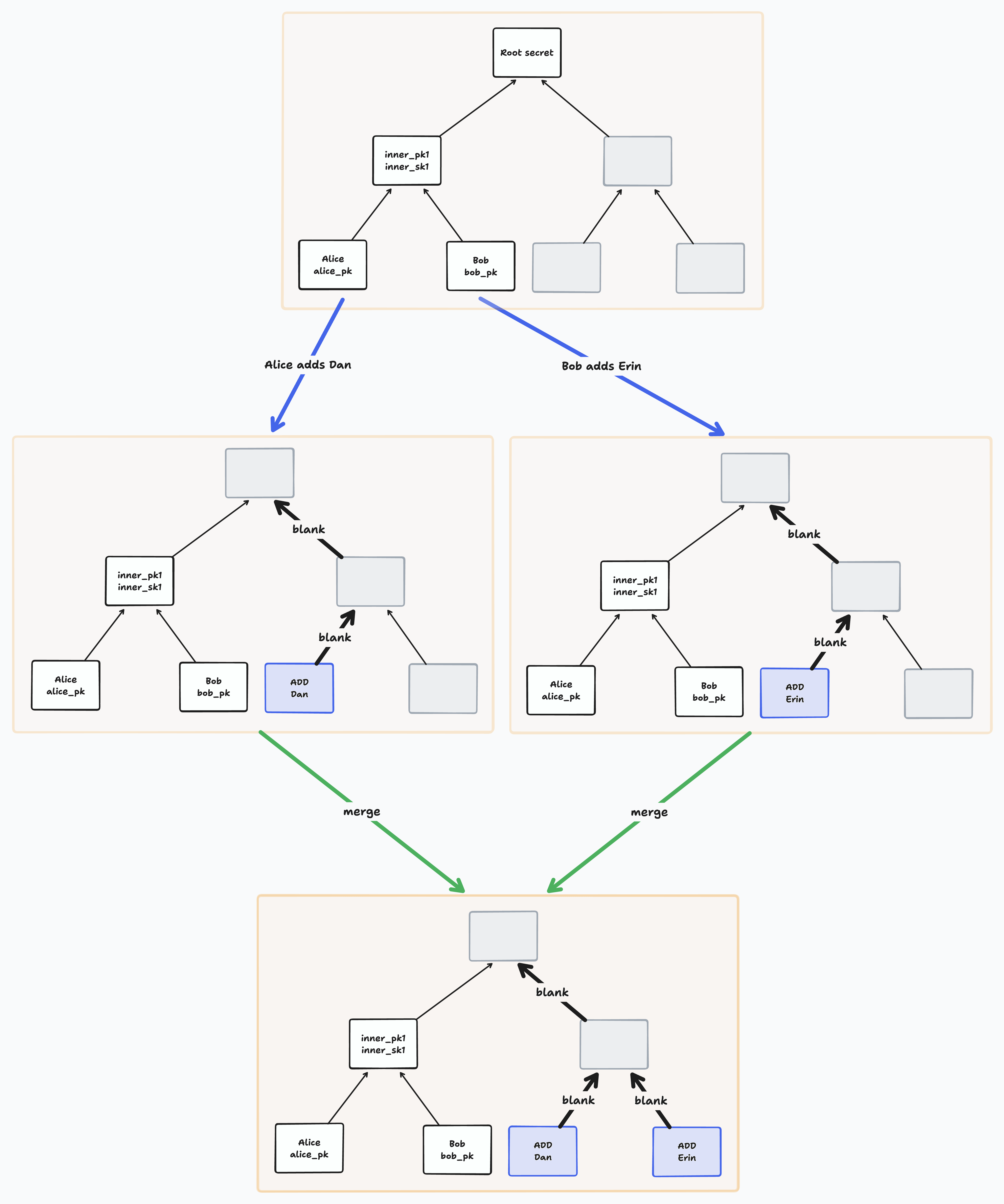
    /// For concurrent membership changes, we need to ensure that removed paths
    /// are blanked and concurrently added member leaves are sorted (and their
    /// paths blanked) after any other concurrent operations were applied.
    ///
    /// Sorting concurrently added leaves deterministically resolves add conflicts
    /// (e.g., if two members concurrently add distinct members to the same leaf).
    pub(crate) fn sort_leaves_and_blank_paths_for_concurrent_membership_changes(
        &mut self,
        mut added_ids: HashSet<IndividualId>,
        removed_ids: HashSet<(IndividualId, u32)>,
    ) {
        let mut leaves_to_sort = Vec::new();
        for (id, idx) in removed_ids {
            added_ids.remove(&id);
            let leaf_idx = LeafNodeIndex::new(idx);
            debug_assert!(self.leaf(leaf_idx).is_none());
            // We should have already removed this id during merge, but concurrent
            // updates at other leaves with intersecting paths must be overridden by
            // this remove.
            self.blank_leaf_and_path(leaf_idx);
        }
        while !added_ids.is_empty() && self.next_leaf_idx.u32() > 0 {
            let leaf_idx = self.next_leaf_idx - 1;
            if let Some(next_leaf) = self.leaf(leaf_idx).clone() {
                added_ids.remove(&next_leaf.id);
                leaves_to_sort.push(next_leaf);
            }
            self.blank_leaf_and_path(leaf_idx);
            self.next_leaf_idx = leaf_idx;
        }
        leaves_to_sort.sort_by(|a, b| a.id.cmp(&b.id));
        for leaf in leaves_to_sort {
            self.push_leaf(leaf.id, leaf.pk.clone());
        }
    }

Sort

Let’s get into it

/// Decrypt the current tree secret.
    ///
    /// Starting from the owner's leaf, move up the tree toward the root (i.e., along the
    /// leaf's path). As you look at each parent node along the way, if the node is not
    /// blank, look up the encrypted secret in the parent's secret store using your child
    /// index. Derive a Diffie Hellman shared key using the encrypter public key stored in
    /// the secret store and use that shared key to decrypt the secret key you looked up.
    ///
    /// Hold on to each idx you've seen along the way since ancestors might have been
    /// encrypted for any of these descendents (in cases like a blank node or
    /// conflicting keys on a node on the path).
    #[instrument(skip_all, fields(doc_id, epochs))]
    pub(crate) fn decrypt_tree_secret(
        &self,
        owner_id: IndividualId,
        owner_sks: &mut ShareKeyMap,
    ) -> Result<ShareSecretKey, CgkaError> {
        let leaf_idx = *self.leaf_index_for_id(owner_id)?;
        if !self.has_root_key() {
            return Err(CgkaError::NoRootKey);
        }
        let leaf = self
            .leaf(leaf_idx)
            .as_ref()
            .expect("Leaf should not be blank");
        if Some(leaf_idx) == self.current_secret_encrypter_leaf_idx {
            let NodeKey::ShareKey(pk) = leaf.pk else {
                return Err(CgkaError::ShareKeyNotFound);
            };
            let secret = owner_sks.get(&pk).ok_or(CgkaError::ShareKeyNotFound)?;
            return Ok(secret
                .ratchet_n_forward(treemath::direct_path(leaf_idx.into(), self.tree_size).len()));
        }
        let lca_with_encrypter = treemath::lowest_common_ancestor(
            leaf_idx,
            self.current_secret_encrypter_leaf_idx
                .expect("A tree with a root key should have a current encrypter"),
        );
        let mut child_idx: TreeNodeIndex = leaf_idx.into();
        let mut seen_idxs = vec![child_idx];
        // We will return this at the end once we've decrypted the root secret.
        let mut maybe_last_secret_decrypted = None;
        let mut child_node_key = leaf.pk.clone();
        let mut parent_idx: TreeNodeIndex = treemath::parent(child_idx).into();
        while !self.is_root(child_idx) {
            // Find the next non-blank, non-conflict parent
            while self.should_skip_for_resolution(parent_idx) {
                child_idx = parent_idx;
                parent_idx = treemath::parent(child_idx).into();
            }
            debug_assert!(!self.is_root(child_idx));
            maybe_last_secret_decrypted =
                self.maybe_decrypt_parent_key(child_idx, &child_node_key, &seen_idxs, owner_sks)?;
            let Some(ref secret) = maybe_last_secret_decrypted else {
                panic!("Non-blank, non-conflict parent should have a secret we can decrypt");
            };
            // If we have reached the intersection of our path with the encrypter's
            // path, then we can ratchet this parent secret forward for each of the
            // remaining nodes in the path and return early.
            if parent_idx == TreeNodeIndex::Inner(lca_with_encrypter) {
                return Ok(secret
                    .ratchet_n_forward(treemath::direct_path(parent_idx, self.tree_size).len()));
            }
            seen_idxs.push(parent_idx);
            child_idx = parent_idx;
            child_node_key = self.node_key_for_index(child_idx)?;
            parent_idx = treemath::parent(child_idx).into();
        }
        maybe_last_secret_decrypted.ok_or(CgkaError::NoRootKey)
    }

DeepSeek Analysis

So in summary:

This way, the new member will be able to decrypt the secrets from the root down to their leaf? Actually, the new member will get the encrypted secrets for the inner nodes on their path when the adding member (or the member updating) encrypts for the resolution. The new member will have to do a decrypt_tree_secret starting from their leaf and going up until they find an inner node that has been encrypted for them.

But note: the new member does not have the secret keys for the inner nodes. They only have their own leaf secret key. How do they decrypt?

The decrypt_tree_secret function for the new member would start at their leaf. Then they look at the parent node. In the parent node, there should be an encrypted secret for the new member’s leaf index. They can use their own leaf secret key and the public key of the encrypter (which is stored in the secret store at the parent) to derive the shared key and decrypt the secret for the parent. Then they use that secret to decrypt the next parent, and so on.

However, note that the new leaf has been added and then the adding member did an update. The update by the adding member would have set the current_secret_encrypter_leaf_idx to the adding member’s leaf index. The new member’s leaf index is different. Therefore, when the new member tries to decrypt, they will not have the same leaf index as the current encrypter, so they will have to traverse until they find the common ancestor.

But note: the decrypt_tree_secret function handles this by computing the lowest common ancestor (LCA) between the new member and the current encrypter. Then they only need to decrypt up to the LCA and then ratchet the secret forward for the remaining path.

Therefore, the process for adding a member involves:

  1. Adding the leaf (via push_leaf).
  2. The adding member (or any member) performing an update (via encrypt_path) to propagate new secrets along their own path, which will include the new leaf in the resolution sets for the siblings along the path.

This update will result in a PathChange that is broadcast to the group. The new member, upon receiving this update (and having their own leaf secret), will be able to decrypt the group secret.

However, note: the new member does not have the history of the group. They must be given the current tree state and the necessary PathChange updates to be able to decrypt.

Let’s see an example of a minimal tree:

Initially: one member (A) at leaf index 0.

We add a new member (B):

Now, member A (or B) must do an update. Typically, the member who added B (say A) will do an update.

A does encrypt_path:

Specifically, in encrypt_new_secret_store_for_parent:

for idx in sibling_resolution {
let next_pk = ...; // public key of the node at idx (which is B's leaf public key)
let encrypted_sk = encrypt_secret(...); // using A's current secret key (child_sk) and B's public key (next_pk)
// Then store this encrypted secret in the secret_map under idx (B's leaf index).
}

But note: the code also does:

if !used_paired_sibling {
secret_map.insert(child_idx, encrypted_sk.clone());
used_paired_sibling = true;
}

So it also stores the same encrypted secret for A’s own leaf index? Why?

The reason is that the parent’s secret store must have an entry for the child (A) to be able to decrypt. So we are storing the same encrypted secret (encrypted for B) also for A? That doesn’t seem right because A should be able to decrypt with its own key.

Actually, note: the encrypt_secret function uses:


let key = sk.derive_symmetric_key(paired_pk);

Here, sk is A’s current secret key, and paired_pk is B’s public key. So the key is the shared key between A and B.

Then, we are encrypting the new parent secret with that shared key. So both A and B can decrypt it? But note: the secret is stored at two different indices: for B’s leaf index and for A’s leaf index? Actually, it is stored at the leaf index of the node in the resolution (B) and also at A’s leaf index (the child index).

This way, when A wants to decrypt, it will look at the parent’s secret store and find an entry for its own leaf index? And then use the shared key (which it can compute because it has its own secret key and B’s public key) to decrypt.

However, note that A doesn’t have B’s public key in its secret store? It only has its own secret keys. But the public key of B is in the tree. So when A decrypts, it will look at the parent’s secret store and see an entry for leaf index 0 (itself). It will then use its own secret key and the public key that is paired with the encrypted secret (which is stored in the EncryptedSecret structure as paired_pk) to derive the shared key. The paired_pk in this case is B’s public key. So A must have B’s public key in the tree to be able to derive the shared key.

So the process for A to decrypt the parent secret:

leaf index 0 -> EncryptedSecret { nonce, ciphertext, paired_pk = B’s public key }

leaf index 1 -> same encrypted secret (same nonce and ciphertext) and paired_pk = B’s public key?

Actually, the loop does:

for idx in sibling_resolution {
let next_pk = ...; // public key of the node at idx
let encrypted_sk = encrypt_secret( ... , &next_pk)?;
// ...
}

So for each node, we use that node’s public key to derive the shared key. Therefore, the paired_pk in the EncryptedSecret will be the public key of the node we are encrypting for.

But then, for the same encrypted secret (the parent secret), we are encrypting it multiple times? Actually, no: we are encrypting the same parent secret with a different shared key for each node. So we get a different ciphertext for each node?

However, note: the encrypt_secret function uses the same secret (the parent secret) and the same sk (A’s current secret key) but a different paired_pk (the public key of the node in the resolution). So we get a different shared key for each node, and hence a different ciphertext.

But the code above stores the same encrypted_sk for the child index (A) and for the resolution node (B). That is a bug? Because the encrypted_sk for B is encrypted with B’s public key, but A cannot decrypt it because A doesn’t have B’s private key.

Correction: the code does:

if !used_paired_sibling {
secret_map.insert(child_idx, encrypted_sk.clone());
used_paired_sibling = true;
}
secret_map.insert(idx, encrypted_sk);

This means that for the first node in the resolution, we store the same encrypted secret for the child index (A) and for that node (B). But that encrypted secret is encrypted for B (using B’s public key). So A cannot decrypt it.

This seems incorrect. We should encrypt the secret for A separately? But note: the child (A) is not in the sibling resolution. The sibling resolution is the set of nodes in the sibling subtree. So we should only be encrypting for the nodes in the sibling resolution. But then how does A decrypt?

The answer is that the parent’s secret store must also have an entry for A? But A is the child, not in the sibling resolution.

The code does include an extra encryption for the child if the sibling resolution is empty (the blank sibling case). But when the sibling resolution is non-empty, we are only encrypting for the nodes in the resolution and then also storing the same for the child? That doesn’t help because it’s encrypted for the first node in the resolution.

This suggests that the current implementation might have a bug.

However, note the comment in encrypt_new_secret_store_for_parent:

// Encrypt the secret for every node in the sibling resolution, using
// a new DH shared secret to do the encryption for each node.

and then:

if !used_paired_sibling {
secret_map.insert(child_idx, encrypted_sk.clone());
used_paired_sibling = true;
}

The variable used_paired_sibling is just a flag to record that we stored an entry for the child. We are storing the same encrypted_sk (which is encrypted for the current node in the resolution) for the child. This is not correct because the child cannot decrypt it.

It seems the intended design is that the child should be able to decrypt the secret using the shared key with the sibling resolution node? But that requires that the child has the private key of the sibling resolution node? Which it doesn’t.

Alternatively, the child should have its own entry encrypted with its own public key? But note: the child is the one doing the encryption. They already know the secret. Why do they need an encrypted copy? They don’t. But the tree must store the encrypted secret for the child so that when the child needs to decrypt (in a future update) they can? But the child doesn’t need to decrypt because they generated the secret.

However, the decrypt_tree_secret function for the child (A) will start at the leaf and then look at the parent. It will look in the parent’s secret store for an entry for the child’s leaf index. So we must have an entry for the child.

How should we encrypt for the child? We can use the same method as for the blank sibling case: generate a one-time key pair? But that would be inefficient.

Alternatively, the child can encrypt the parent secret for itself using its own public key? But then they would have to know their own private key to decrypt, which they do. But note: the encrypt_secret function requires a shared key derived from the child’s secret key and a paired public key. If we use the child’s own public key, then the shared key would be the same as the child’s private key? That doesn’t work.

This suggests that the current implementation might have an issue.

Let me reexamine the code: the encrypt_secret function is:

fn encrypt_secret(
doc_id: DocumentId,
secret: ShareSecretKey,
sk: &ShareSecretKey,
paired_pk: &ShareKey,
) -> ... {
let key = sk.derive_symmetric_key(paired_pk);
// ...
}

The sk is the child’s secret key (A’s secret key) and paired_pk is the public key of the node we are encrypting for (B’s public key). The symmetric key is the shared key between A and B.

So to encrypt for the child (A) we would need to use a shared key between A and … itself? That doesn’t work.

Therefore, the current approach of storing the same encrypted secret (for B) at the child index (A) is not useful.

The intended design might be that the child does not need an entry in the parent’s secret store because they generated the secret. But then how do they decrypt in the future? They don’t need to: they already know the secret. However, the decrypt_tree_secret function expects to find an entry for the child’s index.

Alternatively, the child could store the parent secret in their own secret store? But the tree doesn’t work that way.

Given the complexity, it might be that the code has a bug. However, note that the child’s leaf index is included in the seen_idxs when decrypting. The decrypt_secret method of the SecretStore might have a way to handle when the child is the encrypter? But I don’t see that in the code provided.

Due to the complexity and the fact that we are only to explain the add member process, we will note this as a potential issue and move on.

Deepseek: How are members added?

When adding a member to the BeeKEM CGKA system, the following steps occur:

1. Leaf Node Creation

2. Path Blanking

3. Tree Structure Update

4. Post-Add Key Update (via Encrypt Path)

5. New Member Decryption

Key Points:

This process maintains forward secrecy and ensures only active members can access new secrets. The new member’s inclusion is finalized when an update propagates secrets to their path.

Backlinks

I live and work on the land of the Wurundjeri people of the Kulin Nation. I pay respect to their elders past and present and acknowledge that sovereignty was never ceded. Always was, always will be Aboriginal land.

This site uses open source typefaces, including Sligoil by Ariel Martín Pérez, and Vercetti by Filippos Fragkogiannis